Internal states

If you are reading this page, you are probably wondering how QPLEX actually works. You won't find a complete explanation here. There is no way to fit it all into a software documentation page.

Instead, this page will give you a general idea of the underlying ideas and provide some information about how the software is organized. By examining the source code, you can see exactly what each engine does. But for a formal presentation, you really need to read the QPLEX book.

Let's begin. The previous page introduced a Markov model. In such a model, the pmf of the state of the Markov chain is iteratively computed:

Here v1, v2, v3, ... represent pmfs of the state of the Markov chain at (arbitrary) subsequent time epochs. As noted earlier, these calculations are familiar and precise, but they are also impractical due to the curse of dimensionality.

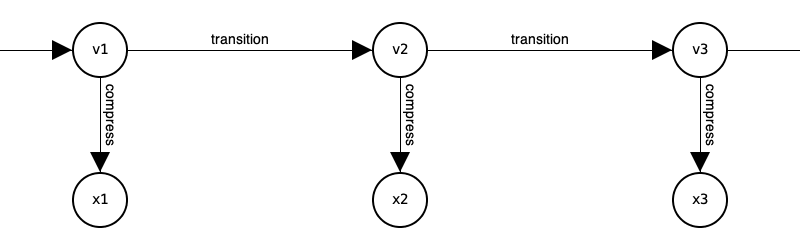
The structure of QPLEX calculations can be similarly represented as

where x1, x2, x3, ... are known as internal states and represent compressed versions of approximations to v1, v2, v3, ... . Working with these internal states is how QPLEX engines avoid the curse of dimensionality. Both the internal state and the step operation are exposed by the engine API.

The compression underlying the QPLEX methodology is lossy and drift-free. To explain what that means, we require the reverse operation, which we call recovery. Lossy means that if a (generic) pmf on the Markov state space is compressed and then recovered, the result is generally not exactly the same as the original. Drift-free means that if a (generic) pmf on the Markov state space is repeatedly compressed and recovered, it never gets worse. In this case, it is possible to make a stronger statement: If an internal state is recovered then compressed, the result is exactly the same as the original. So compressing and recovering many times produces the same result as compressing and recovering once.

A third quality of QPLEX compression is that if a pmf on the Markov state space is compressed then recovered, the result is close to the original. Otherwise, it's of no practical use.

A fourth quality of QPLEX compression is that it retains the marginal probabilities Prob(z) of a pmf on the Markov state space. Only the conditional probabilities of histograms get corrupted to a small extent.

Armed with these insights, let's take a look at some actual internal states in the context of Lesson 4. As seen on the previous page, the pmf of the state of the Markov chain at time 1 is

z	Prob(z)	(2,0,0)	(0,2,0)	(0,0,2)	(1,1,0)	(1,0,1)	(0,1,1)
2	0.30000	0.36000	0.09000	0.01000	0.36000	0.12000	0.06000
3	0.70000	0.36000	0.09000	0.01000	0.36000	0.12000	0.06000

In this table, z represents the number of entities in the system. Each entry in row z and column h represents the conditional probability of state (z, h) given z.

The internal state at time 1 produced by QPLEX is

z	Prob(z)	1	2	3
2	0.30000	0.60000	0.30000	0.10000
3	0.70000	0.60000	0.30000	0.10000

Here's what you should notice:

• The marginal distribution of z (the number of entities in the system) is identical.

• The internal state is smaller than the pmf of the state of the Markov chain (it has fewer columns).

Digging deeper, we make two observations. First, in each row of the Markov state pmf the conditional distribution on histograms h shown in the column headers is multinomial with parameters determined by the corresponding row of the internal state.

Specifically, the distribution

(2,0,0)	(0,2,0)	(0,0,2)	(1,1,0)	(1,0,1)	(0,1,1)
0.36000	0.09000	0.01000	0.36000	0.12000	0.06000

appearing in both rows is multinomial with parameters 2 (the number of servers) and the corresponding row of the internal state

1	2	3
0.60000	0.30000	0.10000

That's the recovery operation; at time 1, the pmf of the state of the Markov chain is the recovered internal state. (Recovery is called multinomial lift in the book, which indeed describes what it does.)

The second observation is that the above row of the internal state is a normalized, weighted average of histograms with the weights taken from the row of the Markov state pmf:

0.36 * (2, 0, 0) + 0.09 * (0, 2, 0) + 0.01 * (0, 0, 2)
  + 0.36 * (1, 1, 0) + 0.12 * (1, 0, 1) + 0.06 * (0, 1, 1) = (1.2, 0.6, 0.2)

The normalization constant is two, the number of entities in service.

That's the compression operation; at time 1, the internal state is the compressed pmf of the state of the Markov chain. It is a lossless compression.

Now let's move on to time 2. The pmf of the state of the Markov chain at time 2 is

z	Prob(z)	(2,0,0)	(0,2,0)	(0,0,2)	(1,1,0)	(1,0,1)	(0,1,1)
2	0.03240	0.36000	0.09000	0.01000	0.36000	0.12000	0.06000
3	0.19440	0.38000	0.08667	0.00778	0.36333	0.11000	0.05222
4	0.39240	0.41367	0.08128	0.00450	0.36826	0.09248	0.03982
5	0.30240	0.47500	0.07222	0.00000	0.37500	0.05833	0.01944
6	0.07840	0.56250	0.06250	0.00000	0.37500	0.00000	0.00000

and the internal state produced by QPLEX is

z	Prob(z)	1	2	3
2	0.03240	0.60000	0.30000	0.10000
3	0.19440	0.61667	0.29444	0.08889
4	0.39240	0.64404	0.28532	0.07064
5	0.30240	0.69167	0.26944	0.03889
6	0.07840	0.75000	0.25000	0.00000

The marginal probabilities of z match, but the rows of the Markov state pmf no longer correspond to multinomial probabilities.

By time 3, even the marginal distributions of z no longer match exactly (although they are still very close). The pmf of the state of the Markov chain at time 3 is

z	Prob(z)	(2,0,0)	(0,2,0)	(0,0,2)	(1,1,0)	(1,0,1)	(0,1,1)
2	0.00350	0.36000	0.09000	0.01000	0.36000	0.12000	0.06000
3	0.03499	0.37200	0.08800	0.00867	0.36200	0.11400	0.05533
4	0.14045	0.38898	0.08455	0.00715	0.36324	0.10669	0.04940
5	0.28755	0.41450	0.07839	0.00545	0.36229	0.09767	0.04169
6	0.31439	0.45621	0.06691	0.00362	0.35536	0.08642	0.03148
7	0.17423	0.53327	0.04429	0.00177	0.33107	0.07188	0.01772
8	0.04145	0.70213	0.00000	0.00000	0.24823	0.04965	0.00000
9	0.00343	1.000000	0.00000	0.00000	0.00000	0.00000	0.00000

and the internal state produced by QPLEX is

z	Prob(z)	1	2	3
2	0.00350	0.60000	0.30000	0.10000
3	0.03501	0.61000	0.29667	0.09334
4	0.14059	0.62395	0.29083	0.08522
5	0.28784	0.64458	0.28021	0.07521
6	0.31405	0.67756	0.25977	0.06267
7	0.17341	0.73555	0.21808	0.04638
8	0.04217	0.84222	0.13338	0.02440
9	0.00343	1.00000	0.00000	0.00000

But wait - didn't we just say that compression retains the marginal distribution of z? Well, it does, but the internal state is not exactly the compressed pmf of the state of the Markov chain.

To see why, we need to delve further into the mechanics of step. To begin, consider the following alternative calculation process for x1, x2, x3, ...:

In this alternative process, the internal state would be exactly the compressed pmf of the state of the Markov chain. But this alternative process is just as impractical as calculating the Markov state pmf directly, because it does compute this pmf directly! And then adds an internal state for decoration.

What QPLEX actually does is more like this:

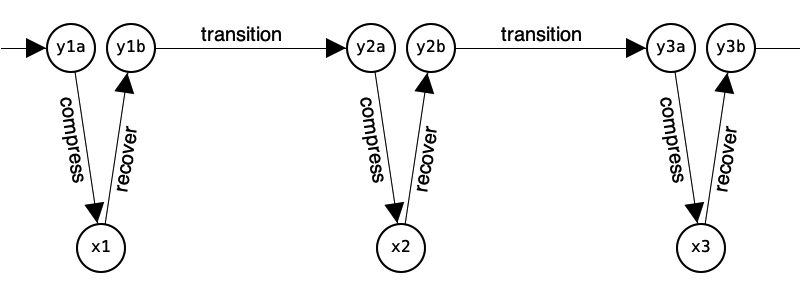
Now step can be mathematically defined as

step(internal_state) = compress(transition(recover(internal_state)))

This is not how QPLEX implements step. Rather, it uses a clever algorithm (which we will not explain here --- read the book!) to avoid enumerating Markov states and calculating transition probabilities, or implementing the recovery, transition, and compression operations.

Now it can be observed that y1a is not the same as y1b because the compression is lossy. (At least in general; compression was lossless at time 1 in our numerical example.) So y2a will not be the same as the pmf v2 of the state of the Markov chain. And x2=compress(y2a) will not be the same as compress(v2).

That concludes the high-level overview. Here are some technical details (in no particular order):

• If L represents the maximum service duration and n is the number of servers, then the number of histograms in a Markov state is \(O(L^n)\). This is also the number of columns in the Markov state pmf (excluding the first two). In contrast, the number of columns in the internal state pmf is only L + 2. So when L is large and n > 1, the reduction will be very significant.

• The internal state is exposed to Python as a dictionary which lists joint probabilities, not conditional probabilities. For example, the internal state at time 1 (see above) appears as

  {(2, 1): 0.18000000000000002, (2, 2): 0.09000000000000001, (2, 3): 0.030000000000000002, (3, 1): 0.42, (3, 2): 0.21, (3, 3): 0.06999999999999999}
  

• In an internal state, the second variable can be interpreted as the remaining service duration of a randomly chosen entity in service. If the remaining durations of all entities in service were assumed to be independent and identically distributed given z, then the histograms would be multinomial. This is the intuition underlying QPLEX's choice of compress/recovery operators.

• A step also prunes the resulting internal state of any values of z for which the probability is less than \(10^{-8}\) and normalizes the remainder. This prevents the internal state size from growing in a way that does not contribute significantly to the results obtained.

• The StandardNetworkMultiserver engine treats each node of a network like a StandardMultiserver engine in isolation, with arrivals from other nodes assumed to be independent. By doing so, it overcomes a second curse of dimensionality due to keeping track of the number of entities at each of the nodes. For details, see Chapter 10 in the book.

• In the StandardMultiserver engine, z represents the number of entities in the system. In other QPLEX engines, it could be something else. For example, a vector. There are lots of examples in the book.

Hopefully, by now, you have an idea how QPLEX actually works: it operates on a pmf (encoded in the internal state) with dramatically fewer entries than a pmf on the Markov state space. An engine's step calculates the next internal state without having to calculate any of the histograms or transition probabilities required of a Markov transition. And that is how it overcomes the dreaded curse of dimensionality.